Special _MIX Reference State¶
pycalphad also includes special mixing reference state that is referenced to the endmembers for that phase with the _MIX suffix (GM_MIX, HM_MIX, SM_MIX, CPM_MIX). This is particularly useful for seeing how the mixing contributions from physical or excess models affect the energy.
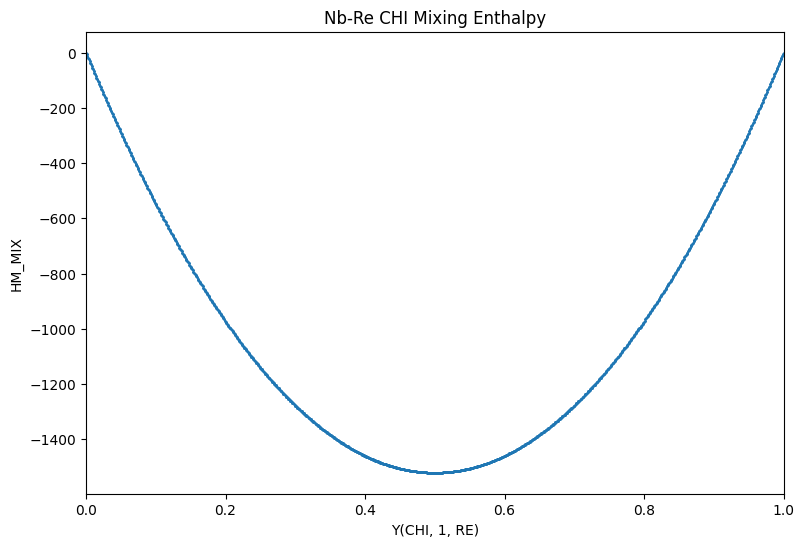
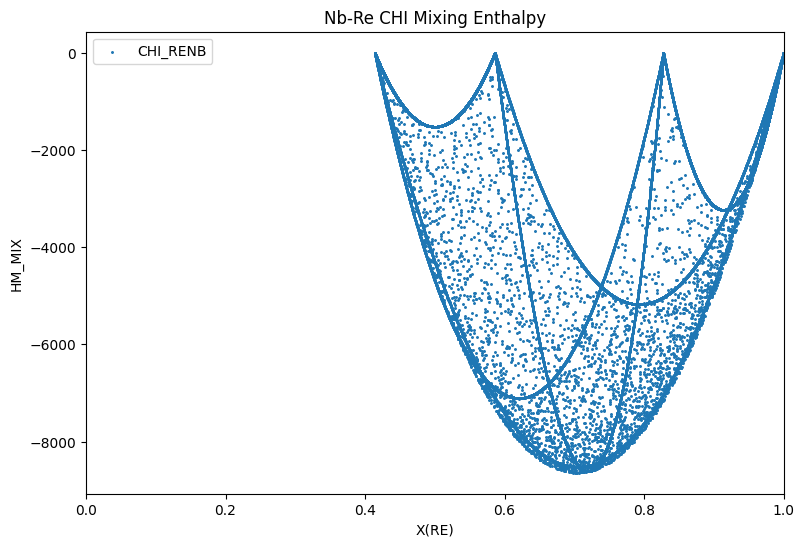
Below is an example for calculating this endmember-referenced mixing enthalpy for the \(\chi\) phase in Nb-Re. Notice that the four endmembers have a mixing enthalpy of zero.
[1]:
from pycalphad import Database, calculate
import matplotlib.pyplot as plt
dbf = Database("nbre_liu.tdb")
comps = ["NB", "RE", "VA"]
# Calculate HMR for the Chi at 2800 K from X(RE)=0 to X(RE)=1
result = calculate(dbf, comps, "CHI_RENB", P=101325, T=2800, output='HM_MIX')
# Plot
fig = plt.figure(figsize=(9,6))
ax = fig.gca()
ax.scatter(result.X.sel(component='RE'), result.HM_MIX, marker='.', s=5, label='CHI_RENB')
ax.set_xlim((0, 1))
ax.set_xlabel('X(RE)')
ax.set_ylabel('HM_MIX')
ax.set_title('Nb-Re CHI Mixing Enthalpy')
ax.legend()
plt.show()
Calculations at specific site fractions¶
In the previous example, the mixing energy for the CHI phase in Nb-Re is sampled by sampling site fractions linearly between endmembers and then randomly across site fraction space.
Imagine now that you’d like to calculate the mixing energy along a single internal degree of freedom (i.e. between two endmembers), referenced to those endmembers.
A custom 2D site fraction array can be passed to the points argument of calculate and the HM_MIX property can be calculated as above.
The sublattice model for CHI is RE : NB,RE : NB,RE.
If we are interested in the interaction along the second sublattice when NB occupies the third sublattice, we need to construct a site fraction array of
# RE, NB, RE, NB, RE
[ 1.0, x, 1-x, 1.0, 0.0 ]
where x varies from 0 to 1. This fixes the site fraction of RE in the first sublattice to 1 and the site fractions of NB and RE in the third sublattice to 1 and 0, respectively. Note that the site fraction array is sorted first in sublattice order, then in alphabetic order within each sublattice (e.g. NB is always before RE within a sublattice)
[2]:
from pycalphad import Database, calculate
import numpy as np
import matplotlib.pyplot as plt
dbf = Database("nbre_liu.tdb")
comps = ["NB", "RE", "VA"]
# The values for the internal degree of freedom we will vary
n_pts = 1001
x = np.linspace(1e-12, 1, n_pts)
# Create the site fractions
# The site fraction array is ordered first by sublattice, then alphabetically be species within a sublattice.
# The site fraction array is therefore `[RE#0, NB#1, RE#1, NB#2, RE#2]`, where `#0` is the sublattice at index 0.
# To calculate a RE:NB,RE:NB interaction requires the site fraction array to be [1, x, 1-x, 1, 0]
# Note the 1-x is required for site fractions to sum to 1 in sublattice #1.
site_fractions = np.array([np.ones(n_pts), x, 1-x, np.ones(n_pts), np.zeros(n_pts)]).T
print('Site fractions:')
print(site_fractions)
print('Site fractions shape: {} ({} points, {} internal degrees of freedom)'.format(site_fractions.shape, site_fractions.shape[0], site_fractions.shape[1]))
# Calculate HMR for the Chi at 2800 K from Y(CHI, 1, RE)=0 to Y(CHI, 1, RE)=1
# Pass the custom site fractions to the `points` argument
result = calculate(dbf, comps, "CHI_RENB", P=101325, T=2800, points=site_fractions, output='HM_MIX')
# Extract the site fractions of RE in sublattice 1.
Y_CHI_1_RE = result.Y.squeeze()[:, 2]
# Plot
fig = plt.figure(figsize=(9,6))
ax = fig.gca()
ax.scatter(Y_CHI_1_RE, result.HM_MIX, marker='.', s=5)
ax.set_xlim((0, 1))
ax.set_xlabel('Y(CHI, 1, RE)')
ax.set_ylabel('HM_MIX')
ax.set_title('Nb-Re CHI Mixing Enthalpy')
plt.show()
Site fractions:
[[1.00e+00 1.00e-12 1.00e+00 1.00e+00 0.00e+00]
[1.00e+00 1.00e-03 9.99e-01 1.00e+00 0.00e+00]
[1.00e+00 2.00e-03 9.98e-01 1.00e+00 0.00e+00]
...
[1.00e+00 9.98e-01 2.00e-03 1.00e+00 0.00e+00]
[1.00e+00 9.99e-01 1.00e-03 1.00e+00 0.00e+00]
[1.00e+00 1.00e+00 0.00e+00 1.00e+00 0.00e+00]]
Site fractions shape: (1001, 5) (1001 points, 5 internal degrees of freedom)