Plotting Isobaric Binary Phase Diagrams with binplot#
These are a few examples of how to use Thermo-Calc TDB files to calculate isobaric binary phase diagrams. As long as the TDB file is present, each cell in these examples is self contained and can completely reproduce the figure shown.
binplot#
The phase diagrams are computed with binplot, which has four required arguments: 1. The Database object 2. A list of active components (vacancies (VA), which are present in many databases, must be included explictly). 3. A list of phases to consider in the calculation 4. A dictionary conditions to consider, with keys of pycalphad StateVariables and values of scalars, 1D arrays, or (start, stop, step) ranges
Note that, at the time of writing, invariant reactions (three-phase ‘regions’ on binary diagrams) are not yet automatically detected so they are not drawn on the diagram.
Also note that the magic variable %matplotlib inline should only be used in Jupyter notebooks.
TDB files#
The TDB files should be located in the current working directory of the notebook. If you are running using a Jupyter notebook, the default working directory is the directory that that notebook is saved in.
To check the working directory, run:
import os
print(os.path.abspath(os.curdir))
TDB files can be found in the literature. The Thermodynamic DataBase DataBase (TDBDB) has indexed many available databases and links to the original papers and/or TDB files where possible.
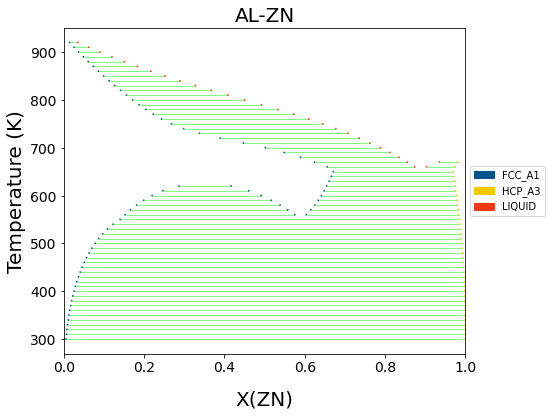
Al-Zn (S. Mey, 1993)#
The miscibility gap in the fcc phase is included in the Al-Zn diagram, shown below.
The format for specifying a range of a state variable is (start, stop, step).
an Mey, Zeitschrift für Metallkunde 84(7) (1993) 451-455.
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
from pycalphad import Database, binplot
import pycalphad.variables as v
# Load database and choose the phases that will be considered
db_alzn = Database('alzn_mey.tdb')
my_phases_alzn = ['LIQUID', 'FCC_A1', 'HCP_A3']
# Create a matplotlib Figure object and get the active Axes
fig = plt.figure(figsize=(9,6))
axes = fig.gca()
# Compute the phase diagram and plot it on the existing axes using the `plot_kwargs={'ax': axes}` keyword argument
binplot(db_alzn, ['AL', 'ZN', 'VA'] , my_phases_alzn, {v.X('ZN'):(0,1,0.02), v.T: (300, 1000, 10), v.P:101325, v.N: 1}, plot_kwargs={'ax': axes})
plt.show()
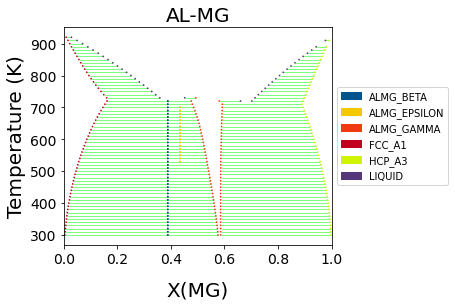
Al-Mg (Y. Zhong, 2005)#
Zhong, M. Yang, Z.-K. Liu, CALPHAD 29 (2005) 303-311 doi:10.1016/j.calphad.2005.08.004
[2]:
%matplotlib inline
import matplotlib.pyplot as plt
from pycalphad import Database, binplot
import pycalphad.variables as v
# Load database
dbf = Database('Al-Mg_Zhong.tdb')
# Define the components
comps = ['AL', 'MG', 'VA']
# Get all possible phases programmatically
phases = dbf.phases.keys()
# Plot the phase diagram, if no axes are supplied, a new figure with axes will be created automatically
binplot(dbf, comps, phases, {v.N: 1, v.P:101325, v.T: (300, 1000, 10), v.X('MG'):(0, 1, 0.02)})
plt.show()
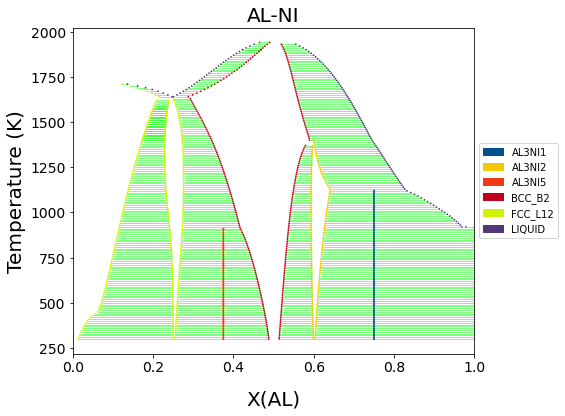
Al-Ni (Dupin, 2001)#
Components and conditions can also be stored as variables and passed to binplot.
Dupin, I. Ansara, B. Sundman, CALPHAD 25(2) (2001) 279-298 doi:10.1016/S0364-5916(01)00049-9
[3]:
%matplotlib inline
import matplotlib.pyplot as plt
from pycalphad import Database, binplot
import pycalphad.variables as v
# Load database
dbf = Database('NI_AL_DUPIN_2001.TDB')
# Set the components to consider, including vacanies (VA) explictly.
comps = ['AL', 'NI', 'VA']
# Get all the phases in the database programatically
phases = list(dbf.phases.keys())
# Create the dictionary of conditions
conds = {
v.N: 1, v.P: 101325,
v.T: (300, 2000, 10), # (start, stop, step)
v.X('AL'): (1e-5, 1, 0.02), # (start, stop, step)
}
# Create a matplotlib Figure object and get the active Axes
fig = plt.figure(figsize=(9,6))
axes = fig.gca()
# Plot by passing in all the variables
binplot(dbf, comps, phases, conds, plot_kwargs={'ax': axes})
plt.show()
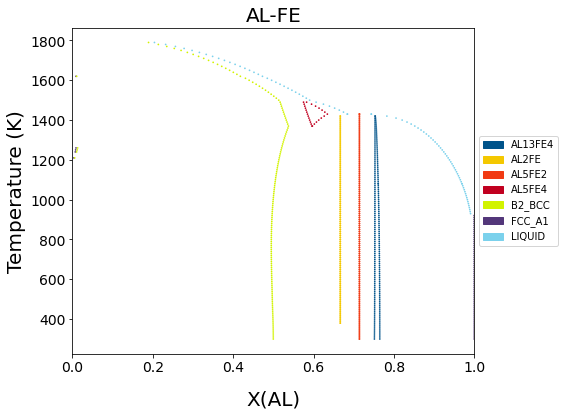
Al-Fe (M. Seiersten, 1991)#
Removing tielines
[4]:
%matplotlib inline
import matplotlib.pyplot as plt
from pycalphad import Database, binplot
import pycalphad.variables as v
# Load database and choose the phases that will be considered
db_alfe = Database('alfe_sei.TDB')
my_phases_alfe = ['LIQUID', 'B2_BCC', 'FCC_A1', 'HCP_A3', 'AL5FE2', 'AL2FE', 'AL13FE4', 'AL5FE4']
# Create a matplotlib Figure object and get the active Axes
fig = plt.figure(figsize=(9,6))
axes = fig.gca()
# Plot the phase diagram on the existing axes using the `plot_kwargs={'ax': axes}` keyword argument
# Tielines are turned off by including `'tielines': False` in the plotting keword argument
binplot(db_alfe, ['AL', 'FE', 'VA'] , my_phases_alfe, {v.X('AL'):(0,1,0.01), v.T: (300, 2000, 10), v.P:101325}, plot_kwargs={'ax': axes, 'tielines': False})
plt.show()
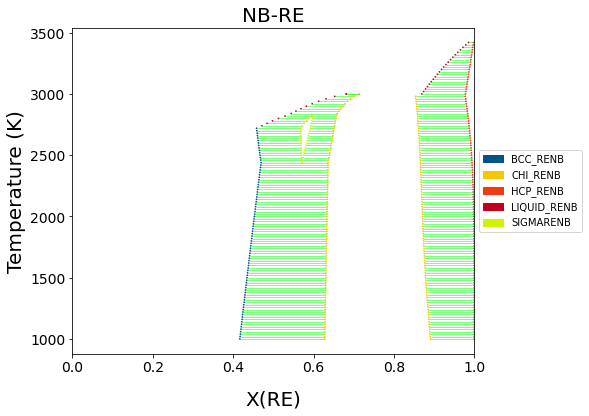
Nb-Re (Liu, 2013)#
X.L. Liu, C.Z. Hargather, Z.-K. Liu, CALPHAD 41 (2013) 119-127 doi:10.1016/j.calphad.2013.02.006
[5]:
%matplotlib inline
import matplotlib.pyplot as plt
from pycalphad import Database, binplot, variables as v
# Load database and choose the phases that will be plotted
db_nbre = Database('nbre_liu.tdb')
my_phases_nbre = ['CHI_RENB', 'SIGMARENB', 'FCC_RENB', 'LIQUID_RENB', 'BCC_RENB', 'HCP_RENB']
# Create a matplotlib Figure object and get the active Axes
fig = plt.figure(figsize=(9,6))
axes = fig.gca()
# Plot the phase diagram on the existing axes using the `plot_kwargs={'ax': axes}` keyword argument
binplot(db_nbre, ['NB', 'RE'] , my_phases_nbre, {v.X('RE'): (0,1,0.01), v.T: (1000, 3500, 20), v.P:101325}, plot_kwargs={'ax': axes})
axes.set_xlim(0, 1)
plt.show()
Calculating Energy Surfaces of Binary Systems#
It is very common in CALPHAD modeling to directly examine the Gibbs energy surface of all the constituent phases in a system.
Below we show how the Gibbs energy of all phases may be calculated as a function of composition at a given temperature (2800 K).
Note that the chi phase has additional, internal degrees of freedom which allow it to take on multiple states for a given overall composition. Only the low-energy states are relevant to calculating the equilibrium phase diagram.
[6]:
%matplotlib inline
import matplotlib.pyplot as plt
from pycalphad import Database, calculate, variables as v
from pycalphad.plot.utils import phase_legend
import numpy as np
# Load database and choose the phases that will be plotted
db_nbre = Database('nbre_liu.tdb')
my_phases_nbre = ['CHI_RENB', 'SIGMARENB', 'FCC_RENB', 'LIQUID_RENB', 'BCC_RENB', 'HCP_RENB']
# Get the colors that map phase names to colors in the legend
legend_handles, color_dict = phase_legend(my_phases_nbre)
fig = plt.figure(figsize=(9,6))
ax = fig.gca()
# Loop over phases, calculate the Gibbs energy, and scatter plot GM vs. X(RE)
for phase_name in my_phases_nbre:
result = calculate(db_nbre, ['NB', 'RE'], phase_name, P=101325, T=2800, output='GM')
ax.scatter(result.X.sel(component='RE'), result.GM, marker='.', s=5, color=color_dict[phase_name])
# Format the plot
ax.set_xlabel('X(RE)')
ax.set_ylabel('GM')
ax.set_xlim((0, 1))
ax.legend(handles=legend_handles, loc='center left', bbox_to_anchor=(1, 0.6))
plt.show()
